
Todos estamos de acuerdo en que cortar la pizza en triángulos con un vértice en el centro es ideal: es rápido; todo el mundo se lleva la misma cantidad de corteza, la misma cantidad de ingredientes; se pueden conseguir cuatro, ocho, dieciséis trozos... Pero los matemáticos siguen buscando alternativas.
Teorizar sobre pizza no es nada nuevo, incluso hay un problema matemático conocido como el teorema de la pizza que se remonta a 1967. Esta vez, los matemáticos Joel Haddley y Stephen Worsley de la University of Liverpool han propuesto nuevas soluciones para otro problema: cómo cortar la pizza en partes equivalentes cuando algunos comensales odian los bordes y otros los adoran.
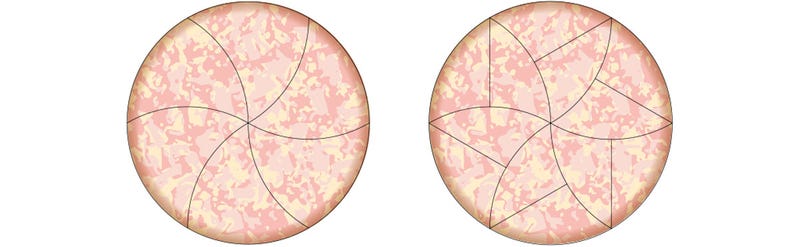
Ya había una solución conocida para este problema: el teselado del disco en mosaico monoedral. Es decir, cortar la pizza en 12 trozos idénticos, de los cuales seis forman una estrella en el centro y los otros seis están en el exterior. Se consigue recortando los trozos con tres lados y después dividiéndolos en dos:
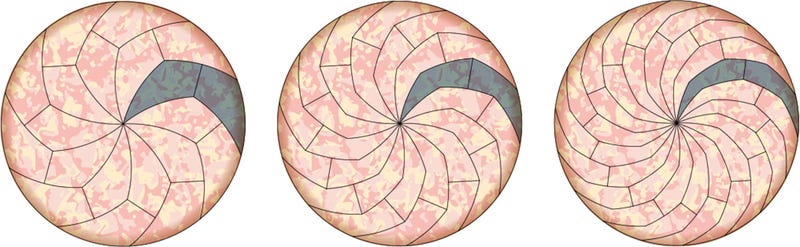
Ahora Haddley y Worsley han encontrado “infinitas” soluciones al problema. La pareja de matemáticos ha descrito una técnica de teselado con la que se pueden conseguir tantos trozos de pizza equivalentes como quieras, sólo hay que recortar cada pieza con un número impar de lados:
Ejemplos con 5, 7 y 9 lados (a partir de 9 puede ser... emmm, poco prático)
Y si lo que quieres es que tus amigos te encierren en un psiquiátrico, también puedes añadir “dientes” a las esquinas de los trozos para conseguir formas más locas, pero igualmente equivalentes:

Comentarios
Publicar un comentario